Evaluating Triple Artemisinin-based Combination Therapies (TACTs) using appTACT
appTACT is an interface for a pharmacokinetic-pharmacodynamic (PK-PD) model that allows you to evaluate the efficacy of different dosing schemes of antimalarial drugs, by simulating drug-parasite interactions in patients infected with malaria. The model is particularly set for Dihydroartemisinin-Piperaquine-Mefloquine (DHA-PPQ-MQ), but essentially, the parameters can be adjusted for studying other drugs combinations as well. Details of the model running in the background can be found in Dini et al. 2018, which is based on the model of Zaloumis et al. 2012 -- if you are interested to know more, read our paper.
The simulations of the model are generated by drawing samples from the parameter distributions presented in clinical trials and in vitro experiments reported in the literature. Using the slider bars in the appTACT (left-side panel), you can vary the medians/means of the parameter distributions (the between-subject and between-isolate variabilities are presented in Tables 2 and 3 of the paper), and then, simulate the model by clicking on the "Simulate the model" button. Note that every time you run the model, you get a different set of responses, as the model is a stochastic model and a different sample is drawn from the parameters space -- this approach aims to mimic the stochastic nature of the underlying biological/physical processes.
Pharmacokinetics
A pharmacokinetic model describes how the concentration of the drug changes in the body after administration. One-compartment models were used for DHA and MQ, and a two-compartment model for PPQ:

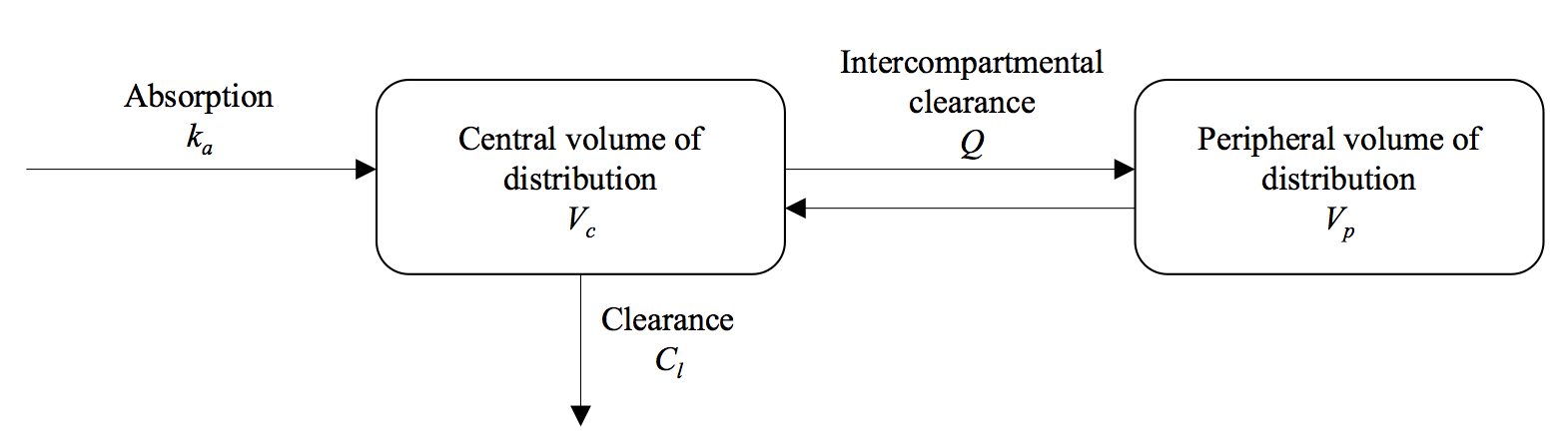
The PK parameter values are drawn from the literature and are provided in Table 2 of Dini et al. 2018. In appTACT, the left figure in the main panel shows the drugs concentrations (on log-scale) over the course of follow-up. In the following, you can find how the killing effect of the drugs is related to these drugs concentrations.
Pharmacodynamics
The pharmacodynamic model describes the time-evolution of the number of parasites in the body, \(N\), by the following difference equations:
$$\begin{eqnarray} N(a,t) = \left\{ \begin{array}{lc} N(a-1,t-1) \left(1 - E(a-1,t-1)\right), & \quad 1 \lt a \leq 48, \\ N(48,t-1) \left(1 - E(48,t-1)\right)\times\text{PMF}, & \quad a = 1, \nonumber \end{array} \right. \end{eqnarray}$$where $a$ is the parasites' age, taking only integer values over $[1~ 48]$, $t$ is time and PMF is the parasite multiplication factor, which represents the number of merozoites released into blood by a shizont at the end of its lifecycle. $E(a,t)$ is the combined killing effect of the drugs which accommodates drug interactions. The combined killing effect of the drugs is between 0 and 1, and dependent upon the age of parasites during $[t, t+1)$. The number of detectable parasites circulating in the blood, $M(t)$, is determined by (Saralamba et al. 2011)
$$\begin{equation} M(t) = \sum_{a=1}^{48} N(a,t) g(a), \nonumber \end{equation}$$where $g(a)$ accounts for the reduction in the number of circulating parasites in the blood due to sequestration, estimated to be
$$\begin{equation} g(a) = \left\{ \begin{array}{lc} 1, & \quad a \lt 11, \\ 2^{\frac{11-a}{3}}, & \quad a \geq 11. \nonumber \end{array} \right. \end{equation}$$The right graph in the main panel of appTACT shows the number of detectable parasites, $M(t)$.
Combined killing effect of drugs
Drugs can interact with each other after their co-administration, which can be synergistic or antagonistic. When drugs have a synergistic interaction, they can produce a stronger combined effect compared to the case where they do not interact, i.e. zero-interaction (aka pure additivity). Antagonistic interaction works the opposite way, i.e. the drugs nullify their additive effect, and produce a lower combined effect than that for the zero-interaction case. Therefore, to be able to model the combined effect, we, first, need to identify interactions between drugs.
MQ and PPQ kill parasites through a similar mechanism, through disruption of haem detoxification in the parasite vacuole. DHA acts differently, by generation of free radicals and reactive intermediates that target various proteins of parasites. Considering these facts (and the concepts of Loewe additivity and Bliss independence explained here ), we define the combined killing effect, $E$, by
$$\begin{equation} E = E_{D} + E_{PM} - E_D E_{PM}, \label{eq:combkill} \end{equation}$$where $E_D$ is the killing effect of DHA and $E_{PM}$ is the combined effect of PPQ and MQ.
For defining $E_D$, we use the well-known Michaelis-Menten formula:
$$\begin{equation} E_D = E_{max,D} \frac{C_D^{\gamma_D}}{C_D^{\gamma_D} + EC_{50,D}^{\gamma_D}} \mathbf{1}_{W_D}(a), \nonumber \label{eq:ekillgen} \end{equation}$$where $E_{max,D}$ is the maximum killing effect of DHA; $C_D$ is DHA concentration; $EC_{50,D}$ is the concentration at which $50\%$ of the maximum killing effect is obtained; $\gamma_D$ is the sigmoidicity (also known as slope) of the concentration-effect curve; $\mathbf{1}_{W}(a)$ is an indicator function, used to implement the age-specific killing of drugs. $E_{PM}$ is defined by
$$\begin{equation} E_{PM} = E_{max,P}\frac{C_{PM} ^{\gamma_P}}{C_{PM}^{\gamma_P} + EC_{50,P}^{\gamma_P}}, \nonumber \label{eq:TallaridaModel} \end{equation}$$ where $$\begin{equation} C_{PM} = \left( C_{P}^\alpha ~\mathbf{1}_{W_P}(a) + C_{eq,M}^\alpha ~\mathbf{1}_{W_M}(a) \right)^\frac{1}{\alpha}, \label{eq:MachadaModel} \end{equation}$$ and $$\begin{equation} C_{eq,M} = E_{P}^{-1} \left( E_{M}(C_{M}) \right), \nonumber \end{equation}$$ where $E_M$ is the killing effect of MQ and $E_{P}^{-1}$ is the inverse of the killing effect of PPQ, given by $$\begin{equation} E_{P}^{-1}(x) = EC_{50,P} \left( \frac{ x}{E_{max,P} - x} \right)^{\frac{1}{\gamma_P}}, \nonumber \end{equation}$$where $E_{max,P}$ and $EC_{50,P}$ are the maximum killing effect of PPQ and the concentration at which half of the maximum killing effect is produced, respectively; $W_P$ and $W_M$ are the killing windows of PPQ and MQ, respectively. Zero-interaction is produced when $\alpha = 1$; the values of $1 < \alpha < \infty$ and $0 < \alpha < 1$ produce antagonism and synergism, respectively. Note that PPQ is considered to be more potent than MQ; see Supplementary Material of Dini et al. 2018 for further information.
PPQ-MQ antagonistic interaction
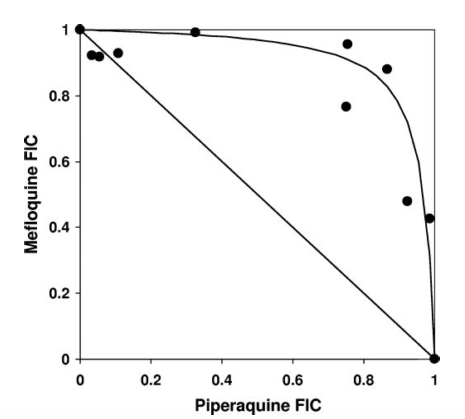
Davis et al. 2006 showed that there is a strong antagonistic interaction between PPQ and MQ. Using the isobologram shown below, they demonstrated that the pairs of drug concentrations that produce a certain effect, say $E_{max}/2$, lie significantly above the linear isobole, indicating a strong antagonism between the drugs.
Parasite resistance to drugs
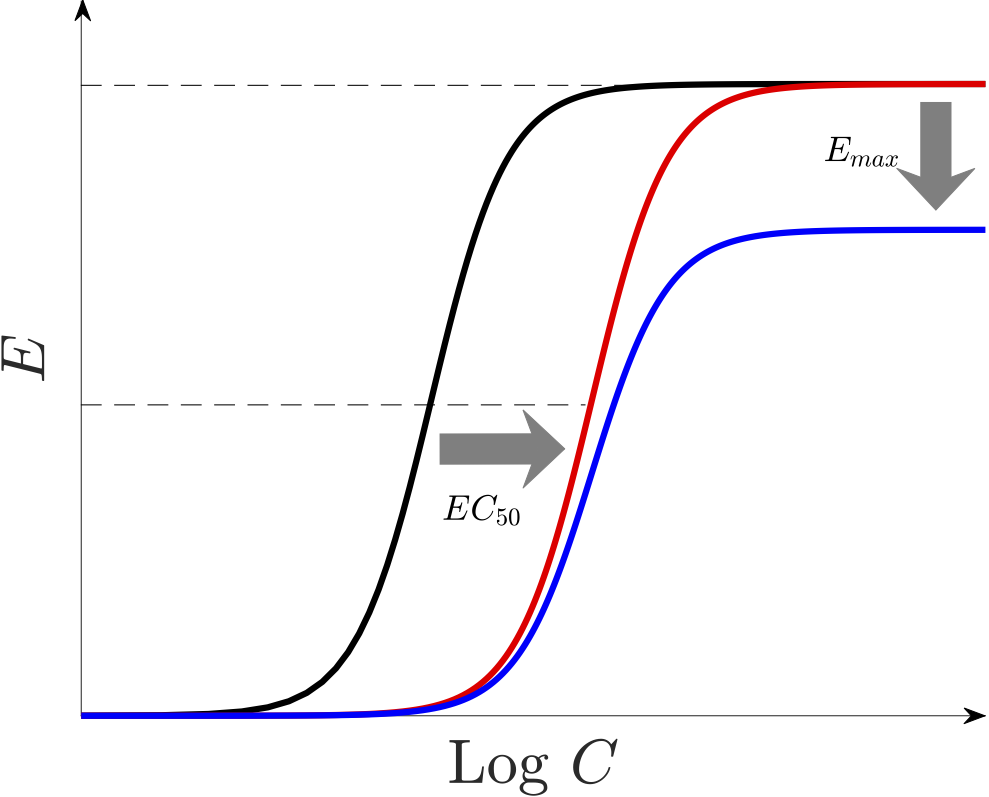
Almost all of artemisinin-based combination therapies (ACTs) are losing their efficacy due to the emergence of resistant parasites to these drugs. By altering the relevant parameters, our mathematical model allows us to investigate various hypotheses on how resistance may manifest and affect drug action. Some of these resistance manifestations include i) increasing $EC_{50}$ (the red curve in below figure), ii) reducing the size of the killing window in the intra-erythrocytic parasite life-cycle, and iii) decreasing $\gamma$ and/or $E_{max}$ (the blue curve).
Now you can go to appTACT and check how varying the PK and PD parameters change the parasitaemia and drug concentration profiles in simulated patients infected with falciparum malaria.